
こんにちは、個別教師Camp事務局です。
さて、前回に続き「テスト勉強の仕方」と題して、前回の内容を、より具体的に書いてみようと思います。
前回は「問題をどう読むか」でした。
第二回目「問題はこう読もう」です。
個別教師Campで使用する実際のテキストから引用して書いていきますのでお付き合い下さい。
先ずは小学生から見ていきましょう!
小学生の問題の読み方
手始めに小5の国語から見ていきましょう。
述語を見つけよう
問題サンプルとして、“ハチの生態”を扱った説明的文章から。
ここで大事なポイントは、後半の「ハチはこの幼虫を何にするのですか。」の部分です。
前回のように主語と述語でとらえると
① 文節に分ける「ハチは/この/幼虫を/何に/するのですか。」
② 述語を見つける「ハチは/この/幼虫を/何に/するのですか。」
③ 述語に対応する主語を見つける「ハチは/この/幼虫を/何に/するのですか。」
しかしこれではまだ分かりにくいのでもう少し付け加えましょう。
「ハチは/この/幼虫を/何に/するのですか。」
ここまで見ていくと問題の意味をとらえやすくなるのではないでしょうか。
答えとしては「何に」するのかを書けばいいのですね。解答は「(例)自分の幼虫のえさ。」となります。
つまり「何に」にという問いに対する「えさ」なのですね。
続いて小6の算数ではどうでしょうか。
尋ねていることと、解くための情報を見極めよう
速さの文章題から。
こういうふうに長い文章が出てきたとき、算数が苦手なお子さんは、もうやる気が消えかけていくのが常です。
しかし落ち着いて見て下さい。この問題文は2文からできています。そして大事なのは後ろの文ですね。
「図書館から駅までの道のりは何mですか。」これです。
これを先ほどのように見てみますと
「図書館から駅までの道のりは何mですか。」
つまり道のりを求める問題です。では前半の文は何なのでしょうか。
先ほど色分けした文だけでは解くための情報が全く不足しています。前半の文は解くための貴重な情報なのです。
考えると分かりますが、なぞなぞで無い限り、無駄な情報はないのです。
何が尋ねられているか、それは何を使って式が立てられるかを必要最小限で書いてあるのです。
それを一見して諦めるのは実にもったいないですね。
ちなみにこの問題の答えは、200×4+80×12 = 1760m となります。
速さ×時間で道のりが求められますよね、これをはじめと残りをそれぞれ求めて足してあるのです。
字数に制限もありますので続けて中学生へまいります。
中学生の問題の読み方
中1の英語ではどうでしょうか。
述語→主語で英文の骨格を作ろう
中1の最初の難関ともいえる三単現の英作文の問題を見てみましょう。
① 文節に分ける「ケンは/あなたの/お父さんを/知りません」
② 述語を見つける「ケンは/あなたの/お父さんを/知りません」
③ 述語に対応する主語を見つける「ケンは/あなたの/お父さんを/知りません」
英語の場合は、ご承知の通り日本語と違い「主語と述語(動詞)」が最初にきましたね。
更に否定文ともなると動詞によって答え方が違い、一般動詞ならば「do(doesやdid)」を使うので、述語部分をもう少し細かく区切ります。
「知り – ません」というふうにです。
さあ、これを英単語に置き換えていきましょう。
繰り返しますが、英語は「主語+述語動詞」です。
「Ken does not know」ができれば、あとは「あなたの/お父さん」をつなげるといいわけです。ココは日本語と同じ語順で大丈夫なので「your father」となりますね。
解答は、
「Ken does not know your father.」となります。基本的にはどんな文法事項であってもこれで解けます。
ここまで駆け足の説明になっているようですが、いかがでしょうか。
続けて中2の数学から。
尋ねていることと、解くための情報を見極めよう
「三角形の合同」から証明問題を見てみましょう。

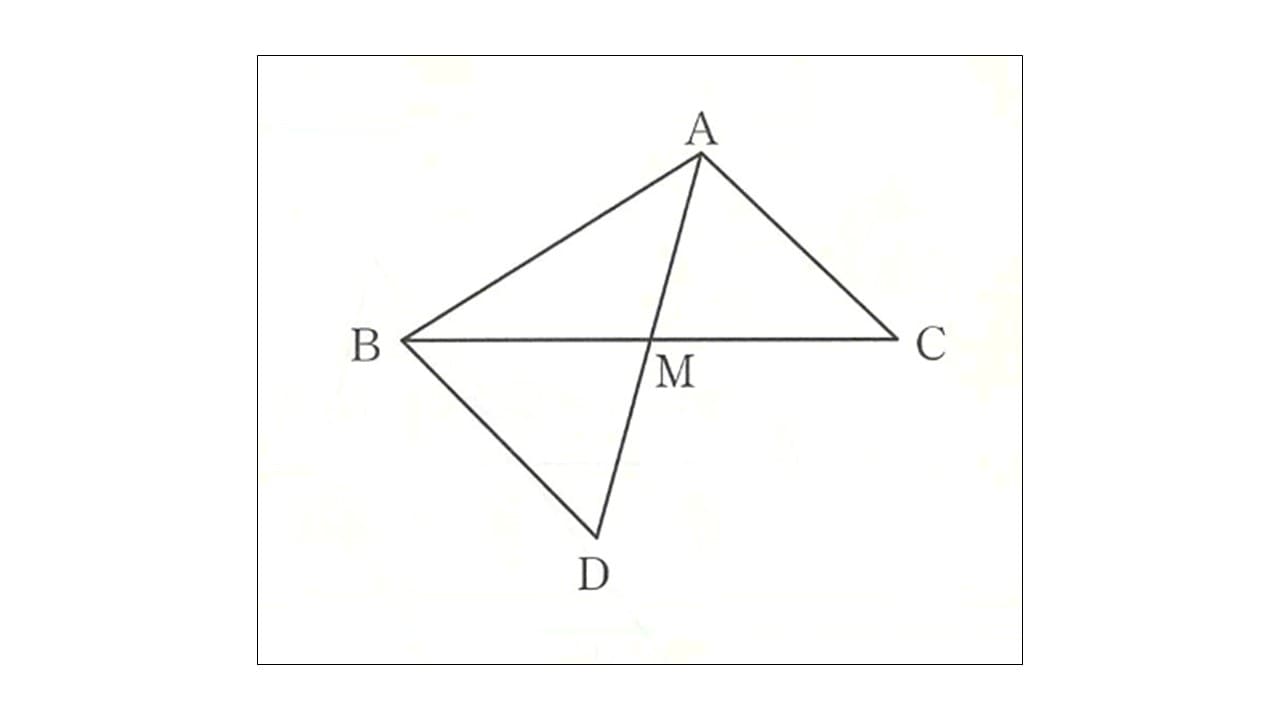
ここまで来るとお子さんたちでも何が問われているかすぐに気付けるのではないでしょうか。
「主語と述語」とは言い難いですが、大事なポイントは「AC=BDとなることを証明」することですよね。
当然、ここまでの文章は上記を証明するための条件(情報)なのです。合同の証明の場合は、「三角形の合同条件」を暗記することが第一です。
そしてどの条件が使えるかを見極めることです。
あとは、合同条件に書かれている条件をその順番で述べていけばよいのです。
解答はこうなります。

この場合は合同条件から「2組の辺とその間の角がそれぞれ等しい」が使えることを見つければ、半分は解けたようなものです。
というのも、この図から分かるのは、辺の長さと対頂角ということだけですね。また辺の長さとは言っても、中点Mで交わる二つの辺すなわち線分ADと線分BCです。
合同条件のうち、二組の辺と対頂角が使えるものは、模範解答にある条件ということになります。
数学の授業になってしまいましたね。
要は、何が問われているかをきちんと読みとること。
もちろん、ここで例示した以上に複雑な問題文はあります。
しかし、基本はそこまで複雑でもありません。
難解に感じるのは、苦手意識が原因であることが多いものです。
落ち着いて取り組むと意外なほどフレンドリーな(!?)問題があります。
ぜひチャレンジしてみて下さい。迷った時は、
個別教師Campまでどうぞ!



