個別教師Campブログ

こんにちは、個別教師Campライターの内海です。

3月14日はホワイトデー！数学の日でもあります！

今年も数学の日にちなんでブログを書こうと思います。

昨年のブログは以下のリンクからご覧ください。

【数学の日にちなんで】円周率を求めてみよう！

0で割ってはいけない理由

何パターンかに分けて、0でわってはいけない理由を考えていきましょう。

①
6÷3=2　⇒　6=2×3

14÷2=7　⇒　14=7×2

このようにわり算はかけ算で表すことが可能です。

しかし、1÷0の場合はどうでしょうか?
この商をⅹとしましょう。
先ほどと同じようにわり算をかけ算で表してみると…
1÷0=x　⇒　1=0　となり、矛盾していることが分かります。

②
1÷3　⇒　1/3

1÷4　⇒　1/4

このようにわり算は分数で表すことができます。
「0でわってはいけないということ=分母が0になってはいけない」になります。

ここで、y=1/xについて考えてみましょう。
これは反比例の式ですので、グラフは双曲線になります。

y=1÷xの表を作成してみると、このようになります。
ここで、x=0の時はどうなるでしょうか。(表中では?としています。)

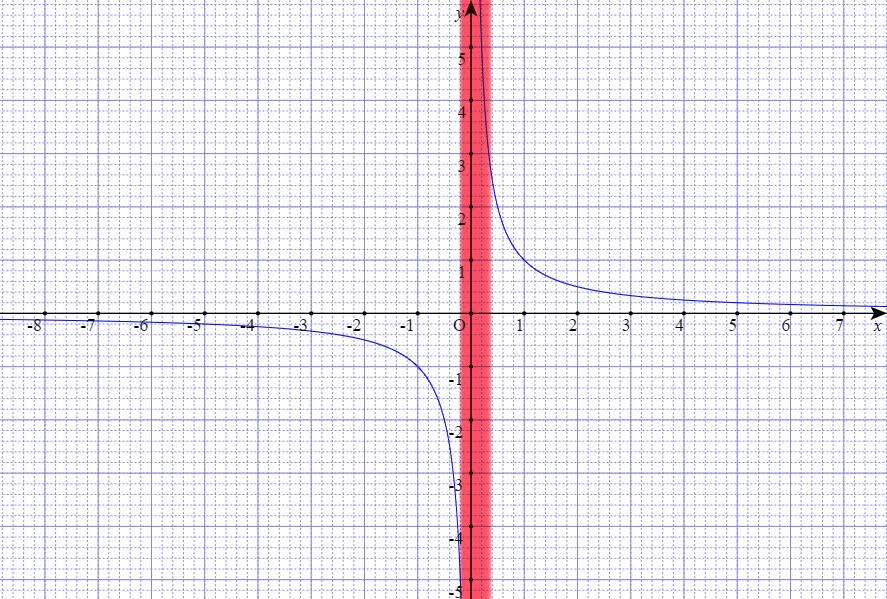
y軸のところを赤で分かりやすくしていますが、x＝0は存在しないのです。

まとめ

今回は0でわってはいけない理由についてブログを書きました。

中学生、高校生でも分かる内容ですので、このブログを読んで理解してもらえると嬉しいです。

初めての方へ