
こんにちは。個別教師Campライターの内海です。
突然ですが、皆さん素数がどんなものなのか覚えていますか? 小学5年生で初めて扱い、中学・高校・大学で素数について詳しく学習していくことになります。そこで、今回は素数の見分け方について書いていこうと思います。
素数とは?
素数とは、「正の約数が1とその数自身である約数で、2以上の自然数」のことを言います。注意しなければならない点として、1は素数ではありませんが、2は素数です。
素数を使う場面
①素因数分解
素因数分解とは、ある自然数を素数のかけ算で表すことで、中1の最初に習う単元です。素因数分解をすることで、正の約数や個数を求めることができます。しかし、どれが素数か分かっていないと、かけ算の形に直すことが難しいです。基本的な素数(20までの素数)は覚えておきましょう。
②平方根
平方根は、2乗すると◯になる値のことを指します。平方根の形から「整数×平方根」や「整数」、「分数」の形にすることが出来ます。
例:√25=√5×5=√5^2=5
√内の数字を素因数分解して、素数の2乗で表すことができれば、それを整数として平方根の外に出すことが出来ます。このように、√の中で素因数分解をするため、素数をしっかり覚えておく必要があります。
素数の見分け方
さて、ここまで素数のことについて簡単に説明してきましたが、いよいよその見分け方についてです。
①消去法
・一の位に注目
一の位が0、2、4、6、8の場合は偶数のため、素数ではありませんので消去できます。また、一の位が5のときも、5の倍数なので消去できます。
・各位の数を足す
各位の数とは、例えば「123」(ひゃくにじゅうさん)であれば、百の位が「1」、十の位が「2」、一の位が「3」ですよね。この「位の数」を足します。「123」であれば、各位の数の和は1+2+3=6となります。
各位の数の和が3の倍数になったならば、もとの数も3の倍数になります。
・7で割る
7の倍数というのも見抜きにくいです。7で割り切れれば、7の倍数であると言えます。逆に、7で割り切れなかったら素数の可能性があります。
・7以上の素数(11、13、17…)で割る
7の倍数と同じ考え方ですが、とくに受験問題などでは11や13はよく出てきます。
②エラトステネスの篩(ふるい)
①の消去法とプロセスは似ていますが、②のほうが視覚的に分かりやすいと思います。
まず、自然数のリスト(表)を用意します。
次に、この表から1を消去します。冒頭でも書いたように、1は素数ではないのでしたね。
そして、2の倍数(水色)、3の倍数(赤色)、5の倍数(緑色)、7の倍数(オレンジ色)を消去します。2の倍数が一番多いので、順番にしていきましょう。一度消したものは確実に素数ではないので、無視してかまいません。
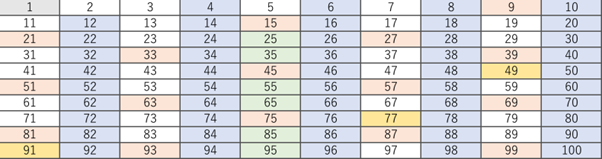
よって、1~100までの素数は2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97の計25個であることがわかりました。
【中学・高校数学】素数の見分け方 まとめ
素数について、理解を深めることは出来たでしょうか? 大学入試には、素数に関する問題がよく出ます。素数の定義や特徴をしっかりおさえて欲しいです。
内海
【略歴】
学生時代から個別指導塾で講師として研鑽を積み、現在は塾講師として就職。最速でena個別の校長に就任し現在に至ります。これまでの指導経験を活かした情報や得意科目である理系科目の情報を中心に発信していきます。大学時代は学芸学部にて数学の微分・積分を中心に研究してきました。これまでに都立三鷹中や調布北高校・武蔵野北高校・多摩大学附属聖ヶ丘高校などの指導実績があります。




